 |
 |
|
||||||||||||||||
����33�� �m�l�v�Z�@�̒��́w�k�x�̌����ƂȂ������J�E���^�[�E�F�C�g���؎��� �O�҂P |
||||||||||||||||
����34�� �m�l�v�Z�@�̒��́w�k�x�̌����ƂȂ������J�E���^�[�E�F�C�g���؎��� �O�҂Q |
||||||||||||||||
����35�� �m�l�v�Z�@�̒��́w�k�x�̌����ƂȂ������J�E���^�[�E�F�C�g���؎��� �O�҂R |
||||||||||||||||
| ����36�� �m�l�v�Z�@�̒��́w�k�x�̌����ƂȂ������J�E���^�[�E�F�C�g���؎��� �O�҂S | ||||||||||||||||
����37�� �m�l�v�Z�@�̒��́w�k�x�̌����ƂȂ������J�E���^�[�E�F�C�g���؎��� �O�҂T |
||||||||||||||||
����38�� �m�l�v�Z�@�̒��́w�k�x�̌����ƂȂ������J�E���^�[�E�F�C�g���؎��� �O�҂U |
||||||||||||||||
|
����39�� �m�l�v�Z�@�̒��́w�k�x�̌����ƂȂ������J�E���^�[�E�F�C�g���؎��� �O�҂V
|
||||||||||||||||
|
����40�� �m�l�v�Z�@�̒��́w�k�x�̌����ƂȂ������J�E���^�[�E�F�C�g���؎��� �O�҂W
|
||||||||||||||||
| �R�D�������� | ||||||||||||||||
| 3�|3�D ���J�E���^�[�E�F�C�g�̕��S�ʐώZ�o�@�@�Â� | ||||||||||||||||
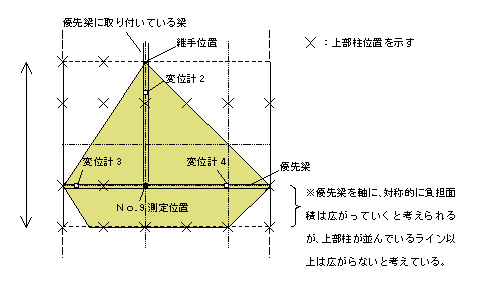
| �i�Q�j�������i����ԍ�No.�X�j�̒��J�E���^�[�E�F�C�g���S�ʐς̍l���� | ||||||||||||||||
| ����ԍ�No.�X�ɂ��Ă͓������Ƃ������Ƃ�����A�Q�e�����̏d�ʂ≮���d�ʁA�ǂ̋Ȃ������Ȃǂ̉e�����l������ƁA�x�����_�������̒��̂悤�ɂ͒��J�E���^�[�E�F�C�g���S�ʐς����߂邱�Ƃ͓���ƍl������B �����ł͏㕔���̈ʒu�ƁANo.�X(�ψʌv�P)�����t�������Ɏ��t���Ă�����̌p��ʒu�Ȃǂ��l�����āA���S�ʐς��Z�肵���B No.�X�����t�������������グ���Ƃ��ɉe������Q�e���ʐς́A���̌p��ʒu�܂ł̒�����㕔���̈ʒu���牺�}�͈̔͂ł���Ƒz�肷��B |
||||||||||||||||
 |
||||||||||||||||
| �����̒��J�E���^�[�E�F�C�g�̕��S�ʐς̍l���� | ||||||||||||||||
| �����������オ�����ƍl������͈� | ||||||||||||||||
| �����������ɂ��āA�ψʌv�Q�̑���ʒu�ŗ��̎����オ�肪���肳�ꂽ�̂ŁA�㕔��������ł��郉�C���܂łł͂Ȃ��A���̌p��ʒu�܂ł̖ʐςƍl�����B | ||||||||||||||||
| �܂������d�ʂɂ��Ă��A���l�̕��S�ʐϕ��̉����d�ʂ����Ȃǂ���āA���J�E���^�[�E�F�C�g�ƂȂ�ƍl�����B | ||||||||||||||||
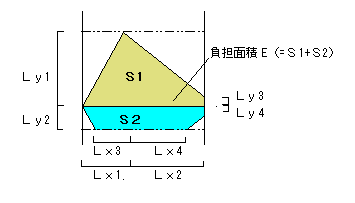
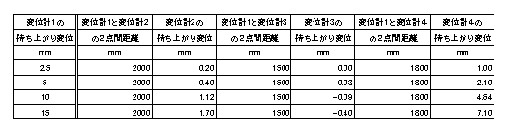
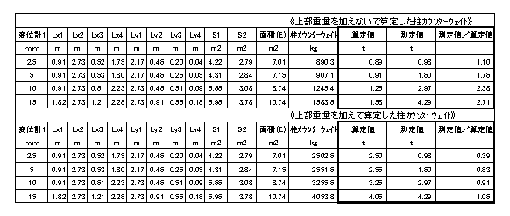
| ������ԍ�No.�X�̑���l�ƕ��S�ʐς��狁�߂����J�E���^�[�E�F�C�g�ɂ��Ă̔�r | ||||||||||||||||
| ���J�E���^�[�E�F�C�g�̕��S�ʐςɂ��Ă͌�o�Q�ƁB ���L�ɎZ��l�Ƒ���l�̔�r�f�[�^�������B ���S�ʐς��狁�߂��钌�J�E���^�[�E�F�C�g�ɂ��āA�㕔������ē`���d���i�Q�e�����̓��ǂ≮���d�ʂȂǁj���S�ʐς̈ڂ�ς��ɔ����A�ǂ�قlje�����ł�̂��킩��Ȃ������̂ŁA���J�E���^�[�E�F�C�g���ȉ��̂Q�ʂ�ɂ��ĎZ�肵�Ă���B �P�D�P�e�����̓��Ǐd�ʂƂQ�e���d�� �݂̂Ƃ����ꍇ �Q�D��L�̏d�ʂɏ㕔�d�ʁi�����d��+�Q�e���Ǐd�ʁj���������ꍇ |
||||||||||||||||
 |
||||||||||||||||
| �����L�̕\�̋L���ɂ��� | ||||||||||||||||
| ��}�̋L���Ɉ�v����B | ||||||||||||||||
 |
||||||||||||||||
 |
||||||||||||||||
| ����ԍ��m��.�X�̒��J�E���^�[�E�F�C�g�Z��l�Ƒ���l�̔�r | ||||||||||||||||
| �s����ԍ�No.9�i�������̏ꍇ�j�̒��J�E���^�[�E�F�C�g�̕��S�ʐς̈ڂ�ς��(1)�t | ||||||||||||||||
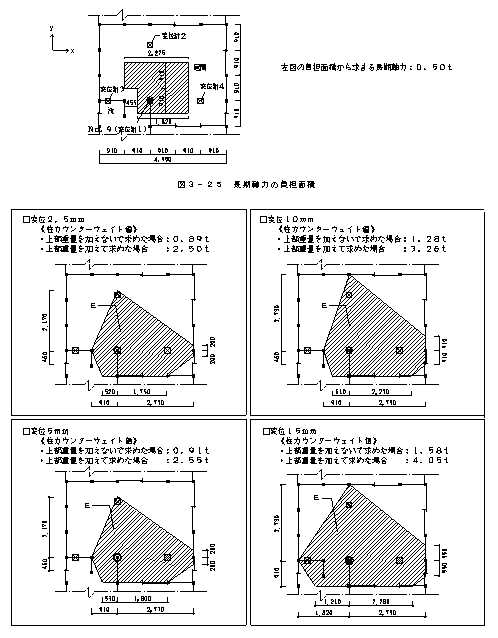 |
||||||||||||||||
| ���̕����オ��ψʂɔ����ĕω����钌�J�E���^�[�E�F�C�g�̕��S�ʐς̍l���� | ||||||||||||||||
| 3�|4�D���J�E���^�[�E�F�C�g�̕��S�ʐςɂ��Ă̍l�@ | ||||||||||||||||
| �i�P�j�x�����_�������̒��Ɏ��t���������iNo.�P�j�ɂ��� | ||||||||||||||||
| No.�P�ɂ����ẮA���̎����オ��ψ�2.5�����`5�����̂Ƃ������I�ɗ��������オ�����ƍl�����ꍇ�A����l�������Z��l��1.5�{�قǂ���A�ψ�10mm���Ă͑���l�ƒ����Z��l�̍����܂��܂��傫���Ȃ�B �e������z���Ă���͒����I�Ȏ����オ����ŕ��S�ʐς����f�������Ă��܂��ƁA���J�E���^�[�E�F�C�g�͏��Ȃ��Z�肵�Ă��܂��̂ŁA�e������Ă���Ɛ��������ψ�10mm�ȏ�͋Ȑ��I�ȖʐώZ�������K�v������B ���̎����オ��ψ�2.5�����`5�����̏ꍇ�ɂ�����1.5�{�̌덷�ɂ��ẮA�ψʌv�R�̕ψ�=�O�Ƃ������Ƃ���A���̎����オ�蒷���ɔ�Ⴕ��X��������Y�������������オ��Ɖ��肵�āA���̎����オ��ψ�10mm�̂Ƃ��̗��̎����オ�蒷�����炻�ꂼ��P�^�S�{�A�P�^�Q�{���āA�ψ�2.5�����`5�����ɂ��Ă����̎����オ�蒷�������߂Ă��邱�Ƃ��e�����Ă���ƍl������B �iNO�D�Q�̑���n�_�̑��茋�ʂ��݂�ƁA�����ʼn��肵���悤�ɒ��̎����オ�蒷���Ɨ��̎����オ�蒷���͕K��������Ⴕ�Ă��Ȃ��̂ł��邪�A���̎������ʂ݂̂ɂĐ������邱�Ƃ͍���ł������̂ŁA����Ƃ��ď�L�ɂ悤�ɎZ��l�����߂��B�j |
||||||||||||||||
| �i�Q�j�x�����_�������̒��Ɏ��t���������iNo.�Q�j�ɂ��� | ||||||||||||||||
| No.�Q�ɂ����Ă����̎����オ��ψ�2.5�����`5�����̂Ƃ����������I�Ɏ����オ�����Ƃ��ĕ��S�ʐς��Z�肵���ꍇ�A�����Z��l�Ƒ���l�����Ȃ�߂��l�ƂȂ��Ă���B �P�Omm�����ꍇ���������A����3���Ȑ��I�Ɏ����オ��ƍl�����Z��l�Ƒ���l���߂��Ȃ��Ă���B No.�P�CNo.�Q�̌v���n�_�ł́A�x�����_�̃R���N���[�g�Ō����傫���R���N���[�g���őS�̂ŕ����オ��ɑ��Ē�R���悤�Ƃ���̂ŁA���J�E���^�[�E�F�C�g�̕��S�ʐς̓x�����_���ʐς͈͓̔��ōl�����A����ȏ�͍L����Ȃ��ƍl������B ���̎����オ��ψʂ�2.5�����`5�����ł́A���J�E���^�[�E�F�C�g�̑���l�̕ω����傫���A�Z�肵�����S�ʐς͕����オ��ψʂɔ�Ⴕ�Ă���B �������A�w�������̎����オ���������E�x�������̎����オ���������͕����オ��ψʂɂ͔�Ⴙ���A�ǂ̔z�u�Ȃǂ��e�����Ă���ƍl������B |
||||||||||||||||
| �i�R�j����ɒ����Ȃ�1�K�������iNO.�X�j�ɂ��� | ||||||||||||||||
| NO.�X�ɂ����ẮA���S�ʐςɂ�������̎����オ����R���Ȑ��I���f�����ɂĎZ�o������Ƃw�E�x�����Ƃ����̎����オ��N�_���p����ʒu�y�ї��̑S����傫�������Ă��܂��A���J�E���^�[�E�G�C�g�̒l���傫���Ȃ肷�����̂ŁA�����I�ȃ��f�����݂̂ɂĕ��S�ʐς��Z�o�����B NO.�X�ɂ����ẮA�Q�K���ʂ������グ��`�ԂƂȂ����BNO.�P, NO.�Q�ƈႢ�A�Q�K���ʂ̍\���͓]�������̏�,����ƂȂ��Ă������ANO.�P, NO.�Q�Ɠ��������ʑS�̂ŕ����オ��ɒ�R���鋓���ƂȂ����B ����ɋߐڂ���Q�K�ǒ��E�Ǔ��ɂ��A���̏�̉����d�������オ���R�͂ƂȂ��ĕψʂ����قǏオ�炸�Ƃ��A�d�����傷�錋�ʂƂȂ����B ���̎����オ��ψʂ�2.5�����`5�����ł́A�㕔�d�ʁi�����d�{�Q�e���Ǐd�ʁj��������Ƒ���l�ɂ���ׂĎZ��l�����Ȃ�傫���Ȃ��Ă���B �������A10mm�ȏ�̕ψʂł́A�㕔�d�ʂ������Ȃ��ŋ��߂��Z��l�͑���l�������Ȃ菬�����A�㕔�d�ʂ��������ꍇ�ł́A�Z��l�Ƒ���l���߂��Ȃ��Ă���B ���̌��ۂ́A�ψʂ��������͈͂ł͒��J�E���^�[�E�G�C�g���̂����قǑ傫���Ȃ��̂ŏ㕔�d�ʂ܂Œ�R�͂Ƃ��Ċ܂܂�Ȃ����A�ψʂ��傫���Ȃ��Ă����ɂꒌ�J�E���^�[�E�F�C�g���傫���Ȃ�A���X�ɏ㕔�d�ʂ܂Œ�R�͂Ƃ��ĉe������Ɛ��������B �i�������A�㕔�d�ʂɂ��Ă͏��ς��d�ɂĎZ�o���Ă���A�㕔�d�ʂɂ��Ă����l�̕��S�ʐς̏d�ʂƂ��ĎZ�o���Ă���B �܂��ANO.�X�̑���ʒu�̑I���ɂ����āA���蒌����ɂQ�e�����Ȃ����ƂƁA���͂Ɉʒu���钌�����Ԉȏ㗣��Ă���Ƃ������Ƃ��l�������̂ŁA���̂悤�Ȍ��ʂƂȂ����ƍl�����邪�A����ɒ������݂�����A���͔��Ԉȓ��ɒ������݂���ꍇ�ɂ́A���̎����オ��ψʂ��������͈͂ł����Ă��A�㕔�d�ʂ���R�v�f�Ƃ��Ċ܂܂��\��������B�j |
||||||||||||||||
| ����̎��������ʂ��������ɂ����ẮA���̕������⍪���̕������Ƃ��������g�݂̕������̈Ⴂ�ŁA���f�����u���ʐςɂ����鍷�ق͐����Ȃ����̂Ǝv����B | ||||||||||||||||
| 4�D�܂Ƃ� | ||||||||||||||||
| ����̎����ł́A�����͂ɂ��ϗ͕ǂɎ��t���Ă��钌�ɕ����オ�肪������Ƃ��̏ォ��̉��������ݗ͂͒��������͂̂悤�Ȓ���{������̕��S�ʐςł͍l�����Ȃ��A���̏㕔�ɓn���Ă���X�����EY�����̗��̎����オ�蒷�����̑傫�ȖʐϑS�̂ŕ����オ����������悤�Ƃ���Ƃ������Ƃ��m�F�ł��A���������͈ȏ�̒��J�E���^�[�E�F�C�g�̌��ʂ����҂ł��邱�Ƃ��m�F�ł����B �܂��A���̕����オ��ψʂ�30mm���x�܂ł́A���̕ψʂ��傫���Ȃ�قǒ��J�E���^�[�E�G�C�g���ǐ����đ傫�Ȓl�ƂȂ�B ���̂��Ƃ͒��J�E���^�[�E�G�C�g�̒l�̑召�ɂ���đϗ͕ǂ̑ϗ͂����E�����Ƃ����W����A��蒌�J�E���^�[�E�G�C�g�̒l�𐳂����]�����邱�Ƃ̏d�v�����Ċm�F�ł����B ����܂ł̒��������͂ł́A�����ɂ����Ă͕��S�ʐς̒l���������Ȃ蒌�J�E���^�[�E�F�C�g�̒l�����Ȃ菭�Ȃ��Z�肳��Ă��邪�A����̑��茋�ʂ��݂�ƕ����オ��ʂ�2.5mm���x�ł����Ă��������͂ɑ��R�D�T�{���x�ANO�D�Q�̑����ł͂Q�{���x������NO�D�X�̓������ł��Q�{���x�ł������B ����ɁA�Q�Omm���x�̕����オ��ψʂł�NO�D�P�̋��p�����̒������͂ɂ����ĂP�P�{���x�ANO�D�Q�̑����ł͂V�{���x������NO�D�X�̓������ł��P�O�{���x�ł������B ���̂��Ƃ͌����S�Ă̒��ɂ����Ă��Ă͂܂邱�ƂƐ�������A�ǂ̗l�Ȓ��ł����Ă��A�Sm���x�̗�������Ώォ��̉��������ݗ͂����҂ł���Ǝv����B �܂��A����̌��ؖړI�ł͂Ȃ����ANO�D�P, NO�D�Q, NO�D�X�ȊO�̒n�_�ɂ��Ă͏���������i�㕔����ǂɂ���R���傫���A���������オ��Ȃ��Ŕ���p�Ƃ��ď��̕����������Ă����j�Ƃ����������A��肭����ł��Ȃ��n�_���������B |
||||||||||||||||
| ����A�����^���ǂ���̏ꍇ�ƃ����^���ǂȂ��̏ꍇ�ɂ��Ď����̔�r���A�����オ��ɑ��ă����^�������Ȃ��R���Ă��邱�Ƃ��m�F�ł����B ���̎����͐ÓI���͎����Ƃ������Ƃ���A�傫�Ȓn�k�ł̃����^�����Ɛ��I�Ȕj�����悤�ȏꍇ�ɂ͓K�p�ł��Ȃ����A�����^�������g�݂Ɩ������Ă���ꍇ�ɂ͐����͂ɑ����R�v�f�Ƃ��čl���ł���Ƃ�����B |
||||||||||||||||
| ���̒��J�E���^�[�E�F�C�g�ɂ��Ă͏Z�E�Z���^�[�ɂ����Ċ�悳��Ă���ϐk�⋭�}�j���A���Ŗ؍\�����z�������@�c������Ă������p�����ɂ��ẮA���S�ʐςƂ����P�Ԋp�i1.82��1.82=3.31�u�j���x�Ƃ������J�E���^�|�E�F�C�g�̑Ó����������ꂽ���̂Ǝv����B �Ȃ��A�������ɂ��Ă͂��̎����ɂ����Ă��𖾂��ꂽ�Ƃ͌�����̂ŁA������Ƃ����v���ɂ����Č�������Ȃ�Ȃ����̂Ǝv����B ���̎����ł͏I�Ǐ�Ԃł���30�������x�i�ό`�p�ł����ƁA�P/�R�O���������x�j�܂Œ��������グ�Ē��J�E���^�[�E�F�C�g�̉e�������A���Ȃ�傫�Ȓ��J�E���^�[�E�F�C�g�l�𑪒�ł��Ă��邱�Ƃ͏�L�ł��q�ׂĂ��邪�A���̂��Ƃ͏I�Ǐ�Ԃɂ����Ă����̕����オ��ɑ��ċ����݂̂Œ�R������̂ł͂Ȃ��A���J�E���^�[�E�F�C�g�̌��ʂ��l���ł���Ƃ������Ƃ��ؖ����ꂽ�̂ł���B ���J�E���^�[�E�F�C�g�Ƃ�����R�͂��l�����邱�Ƃɂ��A���{�×��̓`���\�@�̌����ɂ��Ă��A�ϐk�⋭�ɂ����ċ����ŋٌ������R�@�\�Ƃ��Ȃ��Ă��A������x�͕����オ�낤�Ƃ���͂��������邪�A���J�E���^�[�E�F�C�g�ɂ��|��͖Ƃ��Ƃ������Ƃ��l������̂ł���B |
||||||||||||||||
| ������̎������ʂ̂܂Ƃ� | ||||||||||||||||
| �E�����オ��ɑ��A�����������������Ƃ���͂𒌒������͂ŎZ�肷��ƁA���ۂ̒��J�E���^�[�E�F�C�g�������Ȃ菬�����l�ŎZ�肳���B �E���̎����オ����́A�܂��D����������オ��A�����ėD����Ɏ��t�������������オ��B �̂ɒ��J�E���^�[�E�F�C�g�̕��S�ʐς͗��̎��t�����ɂ���đ傫�����E�����B �E�����オ��ʂ̏��Ȃ��e���͈͓��̕ό`�ł́A���̎����オ����������I�ł���ƍl������B �E���̕����オ�肪�傫���Ȃ�e���͈͂��Ă��܂��ƁA���̎����オ����͂R���Ȑ��I�ɂȂ�ƍl������B |
||||||||||||||||
| ������̎���������̎����q���邽�߂� | ||||||||||||||||
| �E���S�ʐς̉e�����L�͈͂ɂ킽��Ƃ������Ƃ��m�F�ł����̂ŁA�ψʌv�̐��𑝂₷���@�Ƃ��K�v�ł���ƍl������B ���ɓ������ɂ��ẮA���p�����ɂ�����ψʌv�̐��ɑ��ĂQ�`�R�{���K�v�ƂȂ�B �E���̎����オ��N�_����萳�����������邽�߂ɂ��A���ւ̕ψʌv�͕����オ�钌����Ȃ�ׂ��ߋ����i���Ԓ��x�j�ɐ݂���B �E���̎����オ��ɂ��j�؏��ؓ��̌p����̉e����������K�v��������B �E������Ə��ʂ��Ȃ��ꍇ�i����������K�i�����j�ɂ����Ē��J�E���^�[�E�G�C�g��������K�v��������B �E���ƕꉮ���ō\�����ꂽ�����̌��z�\�ʂɂ�钌�J�E���^�[�E�G�C�g�̉e����������K�v��������B |
||||||||||||||||
| �ȏ�̂��Ƃ����ł���A�����S�̃��x���ł��ڍׂȒ��J�E���^�[�E�G�C�g���m�F���邱�Ƃ��ł��A����̐v�@�i���ɏI�Nj��x�v�@�j�ɂ͓��ɗL�v���Ǝv����B | ||||||||||||||||
| �m�l�v�Z�@�̒��́w�k�x�̌����ƂȂ������J�E���^�[�E�F�C�g���؎��� �O�ҁ@�I | ||||||||||||||||
| �������͂�E�܂��遄 �u�؍\�����z������ �c���v��Ɂ@HP: http://www4.kcn.ne.jp/~taharakn ���H�Ƒ�w��w�@ ���z�w�� �q������ |
||||||||||||||||
Copyright(C)
2005 GEKKAN SUGI all rights reserved |
|||